Synchrony Conventions
and the Age of the Universe
This page is about the ways the speed (or lack thereof) of light is measured by two different synchrony conventions: isotropic and anisotropic. Other conventions have been proposed, but they are Sirs Not Appearing In This Film (cue the hairy hand). The isotropic one, or ISC, is the one ordinarily used by physicists; it's a position-independent convention. The anisotropic one, or ASC, is a velocity-independent convention. Jason Lisle of Answers in Genesis proposes that ASC is the biblical one, as described here. If you stumbled on this page without yet having read that one, some of what I say will sound like - well, like a reference to something you haven't read yet. :) That's OK. You can use a wormhole to go back in time and read it before you read this after you read this. Hee hee.
Disclaimer: I'm not a trained physicist. I have no formal training beyond high school physics. But I've always had an interest in the field and done some self-study, and I think I understand the concepts of the synchrony conventions in question. It's certainly possible that I've erred, and if so, I hope that someone will correct me.
Now, using ISC, the starlight we observe today seems to indicate that the universe is several billion years old, since it is considered to have taken that long to reach us from the furthest known galaxies, even taking an expanding universe into account. Using ASC, on the other hand, all starlight is considered to be seen from the earth simultaneous with its emission by each star. Some Young Earth Creationists have concluded from this that our perception of light from distant galaxies thus imposes no particular age requirement on the universe. In this article I raise a question about whether ASC provides any relief from that requirement. None of this should be construed as an argument for the superiority of ISC. My sole point is that ASC may not let us out from under an old universe after all.
I want to make it clear up-front that I'm a Christian and a Creationist, and I have full confidence in the reliability of scripture. I have no interest in undermining the Christian faith or making time for evolution or any of that malarkey. I love and respect my YEC brothers for holding firm to what they believe the scriptures teach. Like them, I'm fully persuaded that a personal, triune God created the universe in the beginning, and that without Him was not anything made that was made. I interpret Genesis literally as history. I don't find that its historical record includes a reference to when God made the universe, however. I think it implies quite unambiguously that the week recounted in the first chapter has a narrower scope. But my interpretation of the text is not the subject of this page. Just wanted you to know where I'm coming from.
The Man and the Mirror. And some flashy thing.
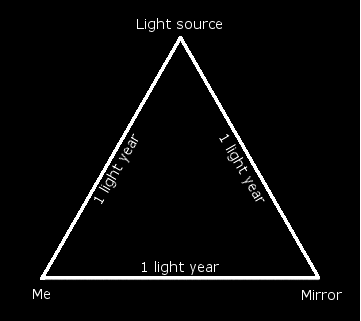
Dr. Lisle did a fine job mapping out ISC and ASC in the theoretical realm. But to grasp its relevance to the age of the universe, it may help to see how both conventions view some more-or-less real-world examples. Really real-world examples would be hopelessly complicated. So we'll strip it down as far as possible. For starters, let's consider the case of three objects at the points of a triangle. We'll make the first one an equilateral triangle with a size of one light year on a side to keep the math obvious. At one corner is a light source. At another is a mirror. At the other is an observer.
We'll call the observer "me" (or "I" as the case requires). When you see "me," don't think me, think you. The point is to place yourself in the experiment imaginatively. That shouldn't be too confusing. If there's anything we learned in school, it's that I am he as you are he as you are me and we are all together. Or if we're not all together, we must be traveling at the same velocity. Either way, that song is now stuck in your head for the rest of the day. You're welcome.
Nobody move!
OK. There are few things we'll assume for the sake of simplicity.
- These scenarios are set in what is effectively a vacuum and a zero-gravity environment.
- The light source is not continuous, but emits a short burst once in a great while, and the light from the bursts radiates from the source in all directions with equal intensity.
- Regardless of the location of the light source, the mirror is always angled just right to reflect the light burst to the intended observer. Convenient contraption, that.
- Any object defined as an observer is always staring unblinkingly at the sky in all directions so as not to miss any perceivable light burst event.
- The terms year and month are extrapolated from those durations as defined by the motions of the earth and heavenly bodies. Those bodies don't come into the following scenarios. If they did, we'd have no end of caveats and complications. Without them, though, there can be no literal years or months within the scenarios themselves. We'll have to import our notions of year and month into the scenarios in order to have familiar terms to use. If we were using only ISC, we could define a year as the length of time it takes light to travel one light year. But for comparing ISC with ASC, that won't work, as you'll see. So, we'll assume that these are equivalent time periods as would be measured by a perfect clock at each of the locations in view. My understanding of special relativity is vague, but I think that definition will be adequate for what we want to illustrate.
- Similarly, a light year in any ASC scenario is the equivalent distance. The definition the distance light travels in one year has no fixed meaning using ASC. But we can import the distance measure the same way we imported the time measure, and as long as nobody moves, no harm, no foul.
So imagine the source emits a burst of light. There's one thing that both conventions agree about: I will see the light directly from the source, and one year after that I will see the reflection in the mirror. What they disagree on is why I perceive that to have happened. Here's the graphic again so you don't have to scroll up and down the page too much.

ISC sees it this way. The source emitted the burst one year before I observed it directly. The light propagated from the source at 186,000 mi/s in all directions. It reached the mirror "at the same time" it reached me, since we're equidistant from the source. The light reflected off of the mirror and traveled toward me at 186,000 mi/s, reaching me one year after it hit the mirror, which was two years after it was emitted by the source (one year from source to mirror plus one year from mirror to me equals two years).
ASC sees it this way. When the source emitted the burst of light, it traveled outward from it at different speeds in different directions relative to me. The light traveling straight toward me had no speed at all by ASC radar. It snuck along the outer edge of the past light cone1 and impinged upon my all-seeing eyeball "at the same time" it was emitted by the source. But as it traveled in other directions relative to me, it propagated at various speeds. It took one year (by my clock) to reach the mirror. At which point it about-faced and hit my eye like a big pizza pie "at the same time" that it hit the mirror.
Both conventions are thought to be perfectly legitimate ways of considering the situation to have occurred. Neither is right or wrong. Each has its advantages and disadvantages, as well as its own paradoxes. Each has its own way of defining what it means for two events to occur at the same time, which is why I put that phrase in quotes above. In fact, a definition of "at the same time" is what a synchrony convention is. Due to the relativity of spacetime, at-the-same-timeness is a disconcertingly ambiguous condition. It's necessary to pick a definition and stick with it for the duration of a given argument. But, strange as it might sound, any definition that makes the math work on paper is a proper one. As counter-intuitive as it feels at first, ASC succeeds in that respect.
On a Clear Day, You Can See Forever
Let's further our grasp of does-anybody-really-know-what-time-it-is by moving our light source a ways out. Imagine that it's two light years from both the mirror and me. Once again, ISC and ASC agree that the reflected light from the mirror will reach me one year after I see the direct light.
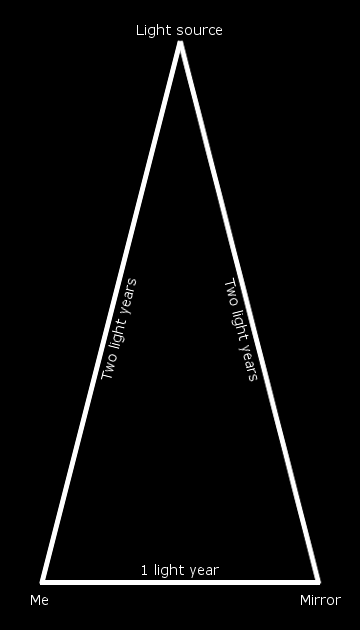
ISC sees this happening. The source emits a burst of light. Two years later, I see the direct light. "At the same time" I see it, it reaches the mirror. The light reflects off the mirror, reaching me one year after that, which is three years after it was emitted by the source. All clear?
ASC considers this to have happened. "At the same time" the burst was emitted by the source, I saw it. The light traveling toward the mirror, however took - uh - hang on. Is something wrong here? We anticipate correctly that I will see reflected light "at the same time" that it hits the mirror. But we've only got one year to work with, here. Does that mean that the light took only one year to reach the mirror from the source, the same amount of time it took to travel half that distance before?! Yup. How could that be? Because we're considering the speed of light to vary with its direction relative to me, and we're counting time by a clock at my position. The light from the repositioned source is traveling in a different direction with respect to me than it did in the equilateral triangle situation. Instead of perpendicular to me, it's now traveling more toward-me-ish. That makes it cover twice the distance in the same amount of (my) time. Weird, huh? Well, as all good Star Trek fans know, it's not one bit weirder than what can happen using ISC. ;)
You can easily extrapolate that, using ASC, the situation is the same for any position of the source along the line created by the first two positions (in other words, any position equidistant from the mirror and me). No matter how far away the source, it will still take none of my time for the light to reach me, and exactly one of my years for the light to reach the mirror - even if it's a billion billion light years away! Freeeeakyyyyy.
What's your angle?
Fleshing out the implications of that, if we place the source somewhere else, at a different distance from the mirror than from me, the light will take a different amount of time to reach the mirror. Depending on the direction that the light travels to reach the mirror, it might take anywhere from a tiny fraction of a second (source almost in a line with the mirror and me, on the other side of the mirror from me) to two years (source at my position or anywhere directly behind me). The only factor in the amount of my ASC-measured time that it takes the light to reach the mirror is the angle. Settle on a given angle with respect to me and you can move the source as close to or as far from the mirror as you like, and the light will take the same amount of my time to reach the mirror. In all cases, the direct light will reach me instantly. Boink. That's some fancy-dancin' light. I like it. It's unapologetically strange.
So now. Apply that to starlight. Light from any star that reaches me obviously came straight my direction, and therefore is seen by me "at the same time" that it was emitted by the star. Yes? Well, yes - using ASC, that is the case because - and only because - that's how ASC defines at-the-same-timeness. So that means it doesn't take any time for light to travel here through space from distant galaxies, right? Not so fast. No pun intended.
Here, I believe, we get the first hint of the possibility of a very sophisticated case of the fallacy of equivocation. You remember, that's where the definition of a term changes in the middle of an argument. The shift in this argument happens to a complex, nearly unspoken term: the frame of reference. The argument begins by showing how light speed may be calculated from the point of view of an individual observer, and then subtly switches points of view to the whole universe for its conclusion without saying so outright. In other words, ASC may well work out fine in asserting that direct light arrives without delay at a particular observer as long as we're only talking about a single observer. But when considering the age of the universe, I'm not sure we can limit our scope that way. Because ASC is position-dependent, it seems to me that when the universe as a whole is the subject, we must consider what would be the case for all potential observers at all potential positions - each of which has its own unique view of what events are simultaneous. And when we try to do that, hoo boy!
Synchronize Watches
To begin to illustrate that, let's add an observer to our scenario. We'll call him "he/him." He lives at the light source, which has been moved to a position one light year from me. However, we'll now move the mirror to my position, pointed at him.

The source emits a burst. Both ISC and ASC agree that he sees the burst at the same time that it is emitted, and that he will see the reflection two years later. Both conventions also agree that I will see the burst at the same time that it strikes the mirror. But that's where agreement ends.
Using ISC, he considers the light to propagate from the source at the speed of light. He counts one year as having passed by the time the light has reached me and struck the mirror. It takes one more year for the light to travel from the mirror back to him for a two-year round-trip. Conversely, from my perspective, when I see the burst of light, I consider it to have been emitted one year prior, and to have traveled the intervening distance of one light year during that time. I calculate that it will take one more year before he sees the reflection. We cannot experimentally confirm our view of the time it took the light to travel there and back again. We can only calculate it based on the assumptions given us by the ISC.
Using ASC, he considers the light burst to take two of his years to reach me and my trusty mirror, because it's traveling straight away from him. Isn't that interesting - it takes twice as long by his clock for light to get from him to me using ASC than using ISC. But it's cool, because he makes up for it by considering the light reflected by the mirror to arrive at his position simultaneous with its arrival at the mirror, correctly yielding the two-year round-trip. That's only his perspective, though. What about mine? When I see the burst of light, I consider it to have been emitted only that moment (by my clock). It took no time on my clock for the light to cover the one light year of distance from the source to me. Also by my clock, he won't see the reflection for another two years after it reaches the mirror, although again, I can't confirm that experimentally, I can only calculate that it must be the case based on ASC assumptions.
Think this through. Using ASC, we both agree that the experiment began with a burst of light from the source, and concluded with his seeing the reflected light burst two years later. We also both agree that light bounced off the mirror during the experiment. But for me, the light hit the mirror "at the same time" it was emitted - at the beginning of the two-year experiment. For him, the light hit the mirror "at the same time" he saw the reflection - at the end of the two-year experiment. This is what it means, practically speaking, for a convention to be velocity-independent rather than position-independent. If two events occur at different positions, they cannot be considered to have happened at the same time as each other for each other. Are you beginning to hear the music?
Now, it's true that we're looking at two clocks separated by a light year, so we can't look at them both at the same time using any synchrony convention. It might seem, then, that all ASC has done is set my clock two years behind his. But what if I had the source and he had the mirror? Then his clock would be set two years behind mine. What if we both had light sources and mirrors? You are now entering the Twilight Zone.
Using ASC, if two events that are distant in space are considered simultaneous as measured by the clock at one of them, their distance in time is twice their distance in light years by the clock at the other. Please keep in mind, this is not a contradiction. It's a paradox created by the decision to define "at the same time" in a particular way. It's no more paradoxical than situations arising from using ISC. Neither clock is set "behind" the other. Each is measuring the travel-time of light from a different direction, and so they arrive at different conclusions. It brings us to the same ultimate conclusions as ISC about what happened. Including, from all I can tell, conclusions about the age of the universe.
Let's Be Mature About This
Suppose a form of our experiment is set at the beginning of spacetime in a YEC-style creation - the universe is abruptly brought into existence in a mature state. At the moment of creation, a lightsource and an observer are brought into being at the same position and the lightsource flashes immediately; same thing one light year away.

Using ISC, he and I will each see the flash from the other's source one year after creation. If I know that his flash happened at creation as mine did, I calculate from the time lag that his source is one light year away. If I determine by some other means that his source is one light year away, I calculate that the flash occurred a year ago at creation. Simple and straightforward. Everything makes good sense.
But this time, ISC and ASC not only disagree about the why question, they disagree about what is going to happen from that point. In fact, ASC seems to disagree with itself. Attempting to use ASC, no matter how we go about it, we run into a logical conflict. Do he and I both see both flashes at the moment of creation? If light takes no time to travel to the observer, we might assume that to be the case. But light also takes two years to get from each of us to the other. Woops.
Do he and I see the other's flash one year after creation, as with ISC? That makes things easier, but it seems arbitrary, and it pulls the rug out from under us if, by some strange chance, we should desire to use ASC to explain how starlight gets to us from more light years away than the universe is old. And we still find that the other's position in the universe was created after our own by our own clock, since the distant flash which occurred at creation was seen one year later, and was simultaneous with its emission. In a universe created mature, this implies that the ASC-defined age of the universe is not a fixed quantity, but is different at any given place for observers in other places. It would seem to follow from this that, using ASC, all parts of the universe have all possible ages from all possible points of observation! Did I say Twilight Zone?
So my position in this weird universe is older than his by my clock, and vice-versa. To put it in universal terms, the minimum age of the universe at any given point out there is relative to its distance from me, regardless of where I am in the universe, and my position is always the oldest. Is ASC giving us a Young Universe-Old Earth view?! Well, kind of, except that the case is reversed for a hypothetical observer out there looking at the earth - he has a Young Earth-Old Universe view.
Here's the reason for the problem. The instantaneous creation of a mature universe means that it was created at all of its myriad positions at the same time. But ASC, being position-dependent, doesn't permit events in different positions to happen at the same time for each other, as we saw in the previous scenario. Casting the event as a mature-creation is the very thing that made it impossible to describe logically using ASC. ASC is incompatible with the description of a universe created mature.
It should be noted that it's perfectly permissible for someone who believes in a mature-creation event to use ASC for some theoretical purposes. He just has to recognize that when he's using ASC, he's not talking about that kind of universe anymore. He can't get back to a moment of creation using ASC - unleeeeess - ah haaaah! maybe he can if it's an event in which all positions are compressed into one. Right? That solves it. Yay.
Um. ::timidly raises hand no higher than top of head:: Isn't there a name for that type of creation event? Huh. Ain't that a kicker? An ISC is fine with a mature-creation event. An ASC implies a Big Bang. Ouch. To get stuff spread out from that dimensionless point to a universe the size we see today takes a wee bit of time. Some billions of years. Aaaaand we're right back where we started.
You see, there's no such thing as a free year, even for light. If you rob the time it takes light to get from somewhere to you, you have to pay it to the time it takes light to get from you to there, as the ASC itself rightly demands. Ultimately, you can't avoid the round-trip. The equation must stay balanced. The time-troll under the light-bridge may let you skip the toll on the way in, but then he will make you pay double on the way out. Or call it the Law of the Conservation of Time. I don't know whether anyone has proposed such a law. Probably not, since it's unnecessary (or transparent, rather) to an ISC. But ASC implies it, doesn't it?
None of this proves that the universe is older than 6000 years. It only means that by examining the universe using a different definition of at-the-same-timeness, we've only piled on more evidence that it is. Older, that is. Way.
NOTES
1Isn't that kind of cheating, though? I don't have the physics chops to develop a specific critique, but pushing the same-time cone infinitesimally outside the past light cone for no clear reason other than to make the model work sounds like fudging to me. I have this nagging suspicion that ASC is getting the light to the observer instantly by having it travel along the boundary of the past light cone and outside that cone at the same time and in the same relation. Did I miss something?
David J. Finnamore
Orlando, FL