|
INTRODUCTION |
| David's Home Page | Tuning Pages Menu | Tuning Methods |
5- TO 9-TONE, OCTAVE-REPEATING SCALES
FROM WILSON'S GOLDEN HORAGRAMS OF THE SCALE TREE
David J. Finnamore
Introduction
The Golden Horagrams area of this site is comprised of 39 HTML pages, 110 images, 15 MIDI files, and 15 mp3 files. I've worked hard to achieve minimum page load times, but for those with dial-up connections of 33 KBs or slower, it might be more convenient to download the zip file (1.02 MB), which includes everything except the mp3 files, and work off of the copy on your hard disk. The mp3s may then be downloaded one by one from that copy.
Whose idea was this, anyway?
I must begin by expressing my indebtedness to Erv Wilson for discovering the Scale Tree and the Golden horagrams that proceed from it, and for meticulously diagramming his discoveries for posterity. Many thanks also to Kraig Grady for getting Wilson to let him publish some of his work on them. Wilson is reportedly a firm believer in the adage, "A picture is worth a thousand words." He draws diagrams - remarkable, insightful, mandala-like diagrams that are at once mathematically sound and profoundly inspired. Some of them he allows to be published in the Wilson Archives of Grady's fascinating and unique web site, Anaphoria Island - without so much as a word of explanation. That, for all their luminescence, can make them somewhat intimidating to investigate.
Thanks also Dan Stearns and Paul Erlich for explaining to me many of the concepts used to analyze the data, and to Robert Walker and Kris Peck for their math help, input, and relentless proofreading. :-)
Speaking only for myself, I'd have to say...
The purpose of this site is to share information about certain scales in Wilson's Golden horagrams of the Scale Tree gained from my own study of them, what I have been told by other people in the process, and what I do with that knowledge. The focus of these pages is on scales with five to nine tones. This introductory page and the key on the following page explain how I arrived at the specific tunings, and define the terminology I use. Some of that terminology is borrowed from others, some I came up with myself. If you know of other terms already in use for the same things, please let me know.
I must emphasize that these pages are not an attempt to explain what Wilson meant by his horagrams (though I'm assured by some who have studied them before that I am on the "right track"). I hope this site helps others see the benefit of the Golden horagrams to tuning theory, and maybe to get a toe hold from which to go on to a deeper and/or different understanding and application of them.
My research has been reasonably thorough in certain specific areas but is not comparable to that necessary for published works of academia. Please consider this a site of personal pages about a hobby topic, not a scholarly treatise on the subject.
The rest of this page gives a brief overview of the application of horagrams to tuning; explains what distinguishes Golden ones, and how they proceed from Wilson's Scale Tree; and defines certain terms as I use them in this context (in bold print). It's not clear to me yet what mathematical characteristics of the horagrams themselves are significant for purposes of tuning and music, and I tend to err on the side of caution - call attention to all possibilities and see what pans out in practice. I've graphically enhanced this explanation and liberally seasoned it with silly puns. If you already understand about all this stuff, you may wish to proceed to the Horagram Menu and Key.
Explanation
Golden Horagrams ... they're not just for breakfast anymore!
Golden horagrams, surprisingly, are not a breakfast cereal. Horagrams are diagrams consisting of concentric circles crossed by a set of radial lines. Fortified by 8 essential vitamins and minerals. They go back at least to medieval times. "Horagram" comes from the Latin "hora," hour. Just as you can see what time it is by observing the angle of the "little hand" on a conventional analog clock (or the shadow on a sundial if you are a medievalist), so you can tell what pitch is indicated by the angle of a radial line on a horagram.
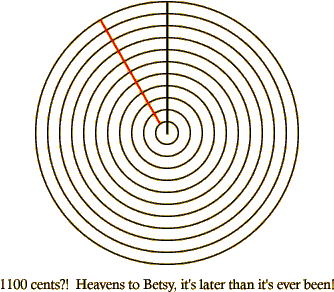
Captain, the generator is on line
It would be possible to construct a horagram from any interval. Let's say you decide to make a horagram using a generator of 100 cents. Start with a bunch of concentric circles. Then make your first radial line from the center at 12 o'clock. If the circle represents a standard octave - 1200 cents - then the next line - the generator - goes at 1 o'clock, beginning on the innermost circle. I like to color the generator red so it stands out from the crowd. The one after that goes at 2 o'clock beginning on the second circle out, and so forth. When you get around the circle, you find that this horagram has reached a dead end: the 13th line would lie on top of the 12 o'clock line, the 14th line on the 1 o'clock line, and so forth. You have a closed system; no new intervals are possible.
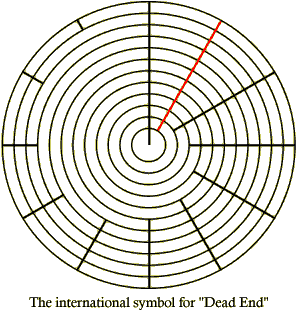
Notice that each ring of the above horagram, except the outermost one, has exactly two step sizes - the generator-sized small steps, and the remainder as a single large step. (The center has only one step size but it's not really a ring, it's just the "core" - the interval that gets divided into scale rings.) This is Wilson's convention (I believe) related to the property he calls MOS, for "Moment of Symmetry." More on that later. For now it's enough to know that each ring of the Golden Horagrams contains exactly two step sizes, and that a new ring is formed whenever a new radial line would divide the current ring into a third step size.
A gold mine of intervals
Notice also that the ratio of large to small step size with this 100 cent generator is always equal to a whole number. That's why it reaches a dead end. When a noble number is used as the generator, the horagram never reaches a dead end. You can keep dividing your intervals smaller and smaller to infinity. Noble numbers involve the irrational number Phi (known in mathematics as the Golden ratio and represented in popular literature by the symbol 
), equal to about 1.618. 
Thus, they always result in two distinct sizes of interval in each ring - one larger and one smaller, and so commonly designated L and s. (Rational generators always lead eventually to a dead end ring containing only one step size.) The two intervals of any given ring of a Golden horagram will have a ratio to each other L:s that bears some relation to Phi - thus, it will never be equal to a whole number. The outer rings always have L:s = exactly Phi; the horagram is said to converge to Gold at the point at which the rings begin to display that property. The ring at which convergence takes place is the ring of convergence, or ROC. The rings displaying the property L:s = Phi are known as Golden rings. I refer to others as alloyed rings since they bear more complicated relationships to Phi, such as 1+Phi or 1+(1/(3-Phi)). Alternatively, Golden rings could be called "outer rings," and alloyed ones be called "inner rings."
A ring number is the number of divisions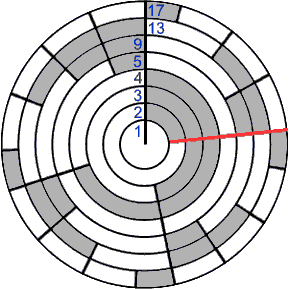
, or of scale steps for tuning purposes, in a ring, not necessarily how many rings it is from the center. The 6th ring from the center in the diagram at left is "ring 9," not "ring 6." This particular horagram has no "ring 6." This is because the 6th, 7th, and 8th radial lines don't produce a third step size in ring 5, so a new ring is not needed until 9.
Wilson numbers what I call alloyed rings on the left hand side of the 12 o'clock line; the Golden rings are numbered on the right hand side. That's nice for seeing the convergence point at a glance, even though the number of the ROC is found directly in the formula, as explained below, so I follow his convention.
Phingering Phi
Phi is pronounced like the English word "fee." It is most succinctly defined as the number whose inversion is itself minus 1.
1/x = x-1
Cute and clever as it is, you can drive yourself to distraction trying to solve that little equation if you don't know how to do quadratics. Take my word for it. Another way to define Phi is with continued fractions:
Phi = 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/ . . . ))))
into infinity. That will get you in the ballpark with a handful of parentheses but you have to carry it to extreme lengths for significant accuracy. Few people have the time or patience to continue the fraction an infinite number of times. People in hell do, of course, but that doesn't do us living folks much good. Thankfully, it's known that Phi also equals:
(SQRT(5)+1)/2
a convenient formula if you have a basic scientific calculator (such as the one that comes with Windows), equal to 1.618033988749894848204586834365638... . There is a distinction between Phi (with a capital P) and phi. They are reciprocal, and have the same value to the right of the decimal point:
1/1.618... = 0.618...
Thus the definition "it's inversion is itself minus 1." It also uniquely has the property that its square is itself plus 1:
2=+1
Weird, huh? It can be useful to picture Phi and its unique properties on a horizontal line:
The line is divided into two sections at B, "phi way" (like 1/2 would yield "half way") from A to C. As the larger division is to the whole line, so the shorter division is to the longer: AC/AB=AB/BC=Phi.1 Savvy? For this reason, its original name may have been the Golden Section. AB and BC have no common factor, no matter how finely you divide them. In mathematical terms, the two sections of the line are incommensurable. As seen in its continued fraction form, it's the factor which provides maximum differentiation. It's the most irrational among irrational numbers.2 That's why you can keep dividing horagram intervals by Phi forever without having one radial line land squarely on top of another.
A phi and a pi became lodgéd
In the crook of a pentacle, so calléd
Said the pi: `Let us phi'
Said the phi: `Let us pi!'
And up popped a Platonic solid!
Hmm, OK, that was quite a stretch. But the number Phi pops up in a most surprising variety of disciplines. In mathematics, it is found to be related to such abstract constructs as the pentagon3, the logarithmic spiral4, and the Fibonacci sequence5. The dimensions and angles of the Platonic solids are related by way of it.6. The famous mathematician Johannes Kepler considered the Golden Ratio to be one of only two "great treasures" of geometry, the other being the Pythagorean Theorem.7 He believed that it "served as a fundamental tool for God in creating the universe."8 Italian Renaissance mathematician Luca Pacioli (1445-1517), who worked with Leonardo da Vinci, went so far as to call Phi the Divine Proportion, and wrote a book by that name about its properties and uses.9
Noble ratios are said to be found in many natural phenomena, such as the relative angles of stems to each other on many plants where it allows each stem maximum exposure to sunlight and rain, and the arrangement of seeds in florets such as the sunflower's, where it allows the seeds to fill space with maximum efficiency10. It's easy to see how that would be useful for plants, but does it really provide a musically useful ratio for scale step sizes? That question can only be answered by trying out such scales and comparing them with other kinds. I think I'm finding that L/s=Phi scales have a general common natureliness, to coin a term. By natureliness, I mean that they have a sort of organic, plasmic, earthy feel to them. This is in contrast to scales built from whole number ratios, which have a sort of angular and abstract feel; and to equal tempered scales with tend to have a sort of 2-dimensional character. At the very least, combined with Wilson's MOS properties, as discussed below, they provide a logical scale system that avoids the pitfalls of both Just Intonation and equal tempered scales.
Multiplying like rabbits
As you look at various Golden horagrams, you'll notice that each L of any given ring is always divided into a new L and s in the next ring out. This is known in mathematics as a rabbit sequence because of the rapid multiplication of intervals that results. You'll also notice that the s size of any given ring is always found in the next ring out, either as its L or its s. When a ring's L size is "received" from the previous ring's s, I call it a mature ring. Kraig Grady put it this way, "The rabbit grows up sometimes slower but once an adult, produces offspring." Keep an eye on them carrots, Elmer.
The ROC is never mature, the rings outside the ROC are always mature (and always Golden). There are often one or more mature rings inside the ROC - such as ring 5 in the horagram above ["Ring numbers"]. Whether maturity is significant to tuning or music is currently very much uncertain. It's just something I noticed and don't want to overlook, in case it does turn out to be meaningful.
Let's all do the Hop
Another good reason to call them rabbit sequences is because of the sort of hop-scotch pattern they produce in diagrams. In the Golden horagrams of the Scale Tree, these patterns relate directly to the formula given by Wilson, as explained below. This is due to the fact that Phi is a continued fraction. When you "hop" out to the next ring, the next portion of the continued fraction is dropped. When you've hopped past a sufficient number of rings to drop all the pieces except Phi, the horagram converges to Gold. Magic.
Golden horagrams don't grow on trees, you know. Oh, wait. Yes they do.
The Noble generators used in the Golden horagrams grow from the branches Wilson's Scale Tree. (Wilson's "tree" looks more like, um, Spanish moss to me, no disrespect intended. I've made a graphic of it that looks more tree-like, which makes it easier for me to follow. David's Tree-like graphic of Wilson's scale tree) Looking at the tree, which can also be found on the first page of Wilson's Golden Horagrams PDF document, you can see that each point on the tree is an intersection of two fractions, a/b and c/d, which I call convergent pairs. Adding the numerators to each other, a+c, and the denominators to each other, b+d, yields a new point at the intersection, (a+c)/(b+d).
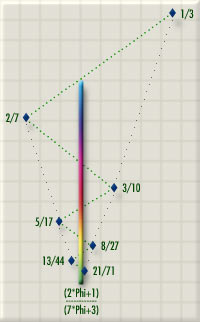
For example, 1/3 and 2/7 intersect at
(1+2)/(3+7)=3/10
2/7 then intersects with 3/10 at 5/17, and so forth. As the tree continues to branch out this way (or to branch down on Wilson's tree and on the image at left), the points on it converge, zig-zag style, toward theoretical points at infinity. Each new point on a branch is closer to the convergence point than the previous ones. To find a convergence point, we plug a/b and c/d into the formula
(c*Phi+a)/(d*Phi+b)
So to find out where 1/3 and 2/7 would eventually converge, we solve for (2*Phi+1)/(7*Phi+3).
Each horagram follows a unique path through the tree. If you were considering six levels of the tree, you could call the zero/one-one/two horagram the
You may note that the only pairs treated as convergent are those that have clear paths between the branches, and that do not cross a nodal center; that is, those that can have a line drawn between them without crossing a branch, and without leaping across from one branch system to another. What about other logically possible pairs? Why not pair up 2/5 with 4/13, for example, or 4/9 with 5/18? Believe it or not, all pairs with unique generator sizes are represented. All other logically possible pairs yield a generator exactly equal to the ones Wilson identified. The tree as drawn exhausts the possibilities. OK, like 32 new tunings weren't enough to keep you busy!
A note on Equal Temperaments on the Tree
Kris Peck pointed out to me that the denominators on a branch of the tree are ring numbers of the corresponding horagram. This is because any given node on the tree represents a whole set of MOS scales generated by an interval that spans a certain number of steps (numerator) of an equal temperament (denominator). For eg. the 5/12 node represents all MOS scales that can be generated by the interval of 5 steps of 12 Equal, or 500 cents assuming division of the 2:1 octave. If a horagram is generated for a node, its ring numbers will be the denominators of each node crossed while climbing the tree to that node. For 5/12, then, the horagram would have rings 1, 2, 3, 5, and 7. 1, 2, and 3 don't really make scales in the traditional sense, which is why a cycle of 12 fifths only provides two MOS scales: a pentatonic and a heptatonic (it provides a whole tone scale, too, but that's not MOS). It follows that prime numbered divisions are richer in scale diversity than composite numbered ones.
The same holds for Phi scales: the ring numbers will be the denominators of every step towards convergence. So the scales in a Golden horagram will have the same numbers of steps and the same step size patterns as those made from the ET generators along its path toward convergence. It follows that if you know, say, the scales generated from 5 steps of 22 ED2, you'll already have a basis for familiarity with Horagram #13 (Wilson's #7),
Following that logic, fully 75% of the tree approximates 5 t-ET, 56% of the tree comes near 7 t-ET, 28% of it comes near 8 t-ET, and so forth. See a bar graph of golden approximations of equal temperaments 5 through 17.
It also follows that the two scales with the same ring number on both branches from any given node will have the same step size pattern. For eg., the generators 5 steps of 22 Equal and 4 steps of 17 Equal will each have a 5 tone MOS LLLLs and a 9 tone MOS LsLsLsLss. So the tree is a useful reference chart whether your medium of choice it ETs or Golden scales.
There are other patterns in the tree and its formula that show up in the Golden horagrams.
- d is the number of the ROC.
- b is the interval between the numbers of the rings on either side of the ROC.
- c is the number of
Lintervals, and a is the number ofsintervals, in each generator-sized division of the second Golden ring (which is the first mature Golden ring). - The ring numbers beyond the second Golden ring proceed in Fibonacci fashion, equaling the sum of the previous two.
- For generators smaller than half the circumference of the circle, which includes all the Golden horagrams, the rings prior to the first complete revolution are different from the rest. It's like the seed grows through the junior part of it's life up until it makes the first complete revolution, at which point it begins to flower and branch out.
- Except for the last of those in the first go-'round, their L-s pattern is a string of generator-sized
s's with a singleLat the end. I call these Gs+R rings, for Generator-s's and Remainder. - The last ring before 12 o'clock is passed for the first time is a string of generator-sized
L's with anson the end. Logically, this is always the innermost mature ring - sort of an adolescent ring, you might say. I call these GL+R rings, for Generator-L's and Remainder. - I refer to both of the above, generically, as GR rings.
- Once the generations have completed a full revolution, all subsequent rings will have L-s patterns that interlace
L's withs's in various ways, and which always have more than one of each interval size. I call these interlaced rings. Any given ring is either GR or interlaced.
- Except for the last of those in the first go-'round, their L-s pattern is a string of generator-sized
So, looking at the formula for horagram #21 (diagram Ring Numbers above), (3*Phi+1)/(13*Phi+4)
- it will converge to Gold at ring 13
- the previous ring inward will be 13-4=9
- the next ring outward will be 13+4=17, and will have 3
L's and 1sin each generator-sized section - the rest of the rings will be 30, 47, 77, and so forth
Doing the Two-step
When drawing a horagram, a radial line begins on the next ring out any time it results in a new step size. Each ring of a Golden horagram will then have exactly two distinct step sizes.
Wilson's term pertaining to single-generator scales of two step sizes is MOS, which stands for Moment of Symmetry (Wilson, 1975). (See definition of MOS in Joe Monzo's online tuning dictionary.) An equivalent term from mathematics is Myhill's property. Another virtually identical term used especially in connection with scales is Well Formed (Carey and Clampitt, 1989). The natural availability of MOS scales is a chief strength of Wilson's Golden horagrams. In my experience, MOS scales tend to make good sense to the ear, and Golden ones most of all.
Does anybody really know what time it is?
There's no law saying that the circle of the horagram has to equal the standard octave. It could represent any Interval of Equivalence that you wish. For instance, if you see an L-s pattern in a ring that looks appealing to you, but would result in intervals too small for scale steps for your taste, why not use an IoE of two octaves? Or three? Or you could make stretched octave scales by setting the circle to 1209 cents. Or you could divide a different ratio such as 3:1, 5:2, or an irrational interval, or whatever you wish. The possibilities are virtually endless - enough for several lifetimes of exploration.
Mine, all mine!
Having now shown you how to spin Gold from the flax of the pitch continuum, I demand that you give me your first-born piece of Phi-tuned music - unless you can guess my true name! [Scampers madly into the distance, cackling and kicking up his heels]
Footnotes: All references are to page numbers in the book The Golden Ratio: The Story of the World's Most Astonishing Number by Mario Livo, ©2002 by Broadway Books, paperback edition.
1: p. 3.
2: p. 85.
3: p. 35.
4: p. 118.
5: p. 101.
6: pp. 66-79.
7: p. 62.
8: p. 154.
9: p. 6.
10: p. 112.
Comments and corrections welcome: tuning@elvenminstrel.com
| INTRODUCTION & EXPLANATION | MENUS | KEY & LEXICON | HEAR EXAMPLES |
