Tuning Methods

Each tuning comprises twelve consecutive composites. Only odd composites are considered due to the assumption of octave equivalence (any even number is regarded as an octave transposition of the odd number obtained by removing all powers of two from it). If you don't assume octave equivalence, your set of composite-only tunings would look very different from these, and you would consider these to be odd-composite-only tunings in distinction from simple composite-only tunings.

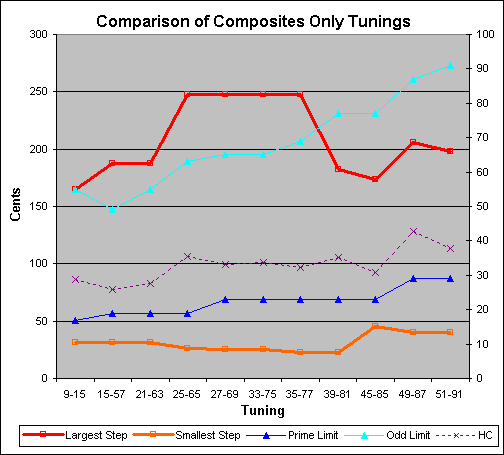
A tuning can only be properly evaluated by ear in a particular musical context with respect to its purpose in that context. Nevertheless, I find it interesting sometimes to compare the numerical characteristics of a set of tunings generated according to the same scheme. The chart below shows that tuning 45-85 stands out as having a surprisingly low harmonic complexity and low contrast between step sizes compared to its neighbors, even though its prime and odd limits no lower. The greatest contrast in step sizes is in the middle set of tunings, rather than at one end as might be expected.